Have you ever wondered how to accurately determine the bending force required for sheet metal fabrication? In this insightful blog post, we will delve into the complexities of bending force calculations, drawing on the expertise of seasoned mechanical engineers. Discover the key factors that influence bending force and learn how to utilize proven formulas to optimize your metal forming processes. Get ready to elevate your sheet metal bending knowledge!
Currently, the commonly used formulas for calculating bending force have been largely derived from foreign sources, often lacking clear information about their origins or applicable contexts.
This article systematically analyzes the derivation process of the bending force calculation formula and outlines the necessary parameters.
Moreover, we will introduce a new approach to calculating bending force, aiming to expand its applicability across various scenarios.
Sheet Metal Bending Force Formula
In recent years, the press brake machine has seen widespread adoption across various industries, significantly enhancing its processing capabilities.
Despite its popularity, there has been a notable lack of systematic discussion regarding the calculation of bending force.
Currently, there are two primary types of bending force calculation formulas recommended by product manuals from different press brake manufacturers:
- P=650⋅S2⋅l / V
- P=1.42⋅S2⋅l⋅σb / V
In these formulas:
- P = bending force (kN)
- S = sheet thickness (mm)
- l = sheet bending length (m)
- V = lower die opening width (mm)
- σb = material tensile strength (MPa)
The recommended formulas for calculating bending force by manufacturers are derived from the formulas mentioned above.
Although these formulas are prevalent in various product brochures, there is often insufficient evidence supporting their accuracy.
Deriving the Bending Force Calculation Formula and Its Applicable Scope
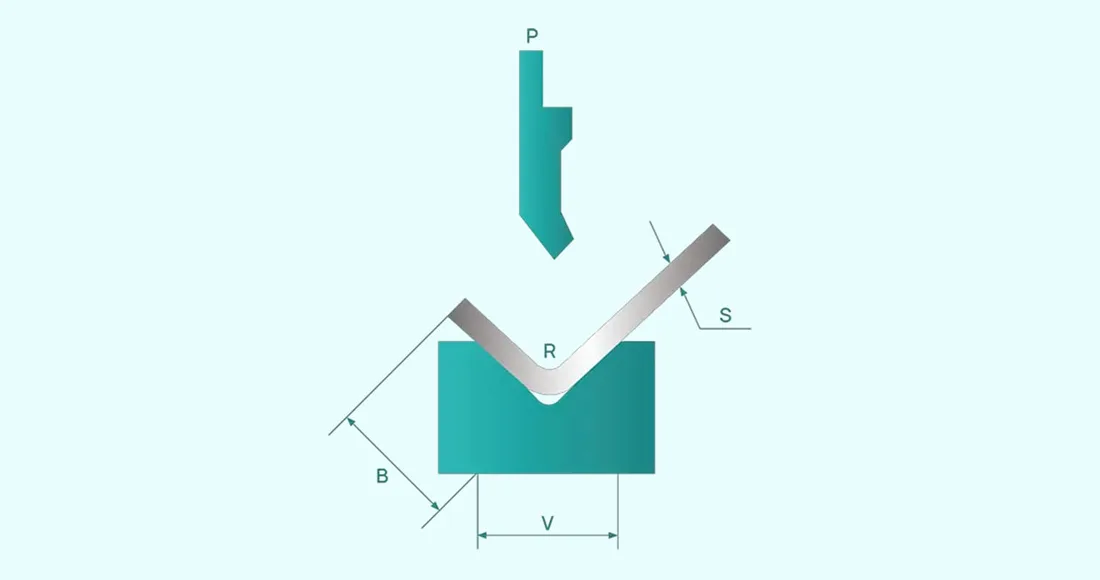
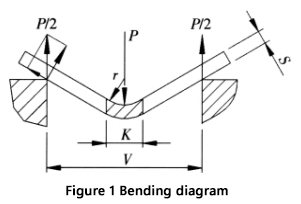
Figure 1 illustrates a schematic representation of the bending process for a sheet.
- P: Bending force
- S: Sheet thickness
- V: Width of the lower die opening
- r: Inner radius during the bending process
- K: Width of the horizontal projection of the deformation zone during bending
The calculation of bending force and its associated parameters are explained as follows:
For free bending, the recommended width of the lower die opening (V) should be 8 to 10 times the sheet thickness (S), with a target width-to-thickness ratio of V/S=9.
Press brake manufacturers typically provide values for the die width (V) and the inner radius (r) of the bent workpiece in their bending force parameter tables. The radius-to-width ratio is usually defined as r=(0.16 to 0.17)V, with the value of 0.16 commonly applied.
During the bending process, the material in the deformation zone experiences significant plastic deformation, allowing it to bend around the centerline. In some instances, small cracks may develop on the outer surface of the curved area.
The stress in the deformation zone, except near the central layer, approaches the material’s tensile strength, with the upper part of the neutral layer under compression and the lower part in tension.
Figure 2 depicts the cross-section and corresponding stress distribution in the deformation zone.
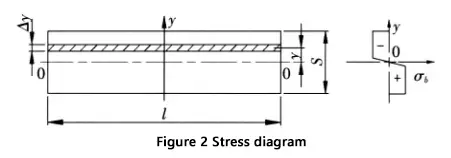
- S: Sheet thickness
- l: Sheet bending length
The bending moment at the section of the deformation zone is expressed as follows:
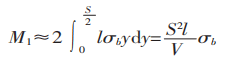
The bending moment produced by the bending force in the deformation zone is illustrated in Figure 1.
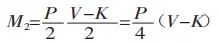
From M1=M2, we derive:

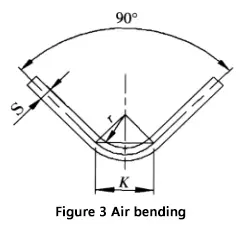
When bending a sheet using a universal mold on a bending machine, as shown in Figure 3, most sheets are bent to 90°. In this case, K is defined as:
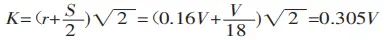
By substituting K into equation (1), we obtain:
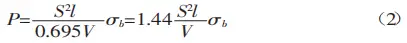
The tensile strength of ordinary materials, σb, is approximately 450 N/mm². This value can be used in formula (2) for calculations.
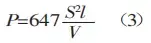
The resulting formula for calculating bending force aligns with the information provided in foreign brochures.
The variables in this formula include:
- S: Sheet thickness
- r: Inner radius during bending
- K: Width of the horizontal projection of the bending deformation zone
From the derivation process, it is essential to meet two additional conditions when using formulas (2) or (3) to calculate bending force: the width-to-thickness ratio (V/S) must equal 9, and the radius-to-width ratio must equal 0.16.
Failure to satisfy these conditions may lead to significant errors in calculations.
New Methods and Steps for Calculating Bending Forces
The calculation of bending force can become complex when the two additional requirements (width-to-thickness ratio V/S=9 and radius-to-width ratio = 0.16) cannot be met due to design or process constraints.
In such cases, it is advisable to follow these steps:
- Calculate the Width-to-Thickness Ratio and Radius-to-Width Ratio:
Use the sheet thickness (S), bending radius (r), and lower die opening width (V) to determine these ratios. - Determine the Projection Width of the Deformation Zone:
Consider the effects of sheet deformation when calculating the projection width of the deformation zone. - Calculate Bending Force Using Formula (1):
Apply formula (1) to compute the bending force, incorporating any differences in the bending radius and the corresponding deformation zone.
By following these steps, you can achieve a more accurate and reliable result compared to using the commonly accepted formulas. An example to illustrate this process is provided in Figure 4.
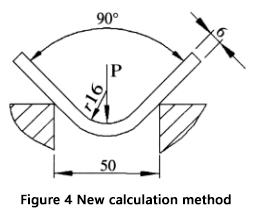
Example:
- Sheet thickness (S) = 6 mm
- Sheet length (l) = 4 m
- Bending radius (r) = 16 mm
- Lower die opening width (V) = 50 mm
- Material tensile strength (σb) = 450 N/mm²
Question: How Can We Calculate the Bending Force Required for Air Bending?
Here are the steps:
- Calculate the Width-to-Thickness Ratio and Radius-to-Width Ratio:
Begin by determining these ratios based on the sheet thickness and the dimensions of the lower die opening.
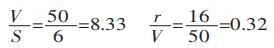
- Calculate the Projected Width of the Deformation Area:
Assess the projected width of the deformation area considering the sheet's deformation during the bending process.
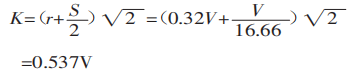
- Calculate Bending Force Using Formula (1):
Finally, apply formula (1) to compute the bending force required.
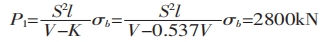
If the commonly recommended formula is used to calculate the bending force, it can be inferred that:P1/P2=1.5
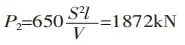
This indicates that the difference between P1 and P2 is 1.5 times greater.
The reason for this discrepancy is that, in this example, the bending radius is relatively large, resulting in an increased deformed area and, consequently, a higher required bending force.
In this case, the radius-to-width ratio is 0.32, which exceeds the previously mentioned criteria.
Using the standard formula for calculating bending force is not suitable for this scenario. The advantages of employing the new calculation method become evident through this example.
Additionally, there is an online calculator available to compute the bending force using this new method.
Tensile Strength Table
| Material | Tensile strength | ||
|---|---|---|---|
| American | European | China | N/mm² |
| 6061 Aluminum | Alu50 | LD30 | 290 |
| 5052 Aluminum | Alu35 | LF2 | 303 |
| 1010 Mild steel | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| 304 Stainless | Inox V2A | 0Cr18Ni9 | 586 |
| 316 Stainless | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Low alloy | 42 CrMo 4 | 42CrMo | 1000 |
Bending Force Calculation Formulas for Coining
The formulas for calculating coining parameters differ from those used in air bending:
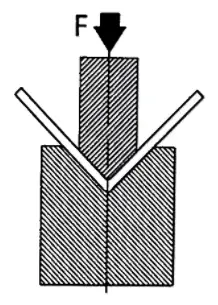
- Width of the Die Vee:
V = sheet metal thickness × 5
- Internal Radius:
The internal radius is determined by the punch tip and should be calculated using the following formula:
Radius = sheet metal thickness × 0.43
- Force Required for Coining:
The force required for coining can be calculated as follows:
F(kN/m) = Thickness2 × 1.65 × Tensile Strength(N/mm2) × 4.5 / Die Vee Width
- Minimum Internal Edge:
The formula for calculating the minimum internal edge remains the same:
Minimum Internal Edge = Die Vee × 0.67
Bending Force Calculation Formulas for Z-Bend
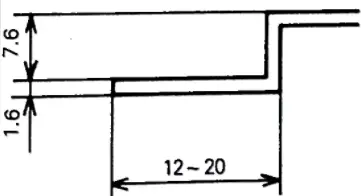
Certain tools require specific force to yield the sheet metal and manage springback to achieve the desired profile.
For instance, consider joggle tools, which create two bends simultaneously with a short distance between the bend and the counterbend. Since these tools perform two bends at once, springback must be completely countered by coining.
The equation to calculate the necessary force is:
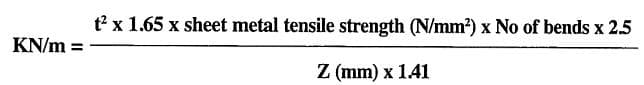
Where:
- KN/m = necessary force per meter
- Z = joggle in mm
- No of bends = 2 for a Z-bend
Joggle tools typically consist of an insert holder into which the selected joggle tools are secured using grub screws, based on the desired joggle and angle.
It is crucial to seek technical advice from the manufacturer before making a purchase, as these systems are designed for bending thin sheet metal, with a maximum thickness of 2 mm. However, the actual maximum thickness may depend on the type of insert used and could be less than 2 mm.
Conclusion
The formulas and steps provided for calculating the bending force are applicable not only to angular bending of sheets but also to arc-shaped bending, which is technically considered angle bending with a large bending radius.
It is essential to remember that forming an arc shape necessitates a specialized mold design. When projecting the deformation area, calculations must be based on the specific process parameters established during fabrication, as these cannot be determined through a single formula.
For example, at a specific iron tower factory, we successfully bent a cylinder with a wall thickness of 12 mm, a diameter of 800 mm, and a length of 16 m using a 28,000 kN press brake machine and a circular mold. The methods outlined in this article were employed to calculate the bending force, resulting in satisfactory outcomes during the mold design process for the arc shape.